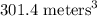Answer: A)
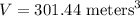
B)
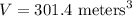
Explanation:
Given: The radius of cone = 6 meters
the height of cone = 8 meters
We know that the volume of cone is given by :-
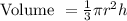
Therefore, the volume of given cone will be :_
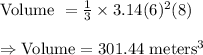
The exact value of the volume of the cone:
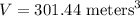
Also,
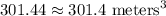
Thus, the approximate value of the volume of the cone to the nearest tenth:
V=