Answer:
The probability that a randomly selected student’s math score is between 300 and 700 is 0.9544.
Explanation:
We have given that, The SAT mathematics scores in the state of Florida are approximately normally distributed with a mean of 500 and a standard deviation of 100.
To find : What is the probability that a randomly selected student’s math score is between 300 and 700?
Solution :
The mean is
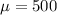
The standard deviation is
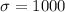
Formula to find z-score is
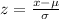
Now, we have to find the probability score is between 300 and 700
For x = 300 substitute in the formula,
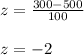
For x = 700 substitute in the formula,
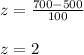
Now, The probability between P(-2<z<2) is written as
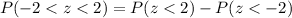
Using the z table substitute the values of z
At z<-2 is 0.228 and at z<2 is 0.9772.
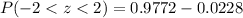
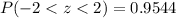
Therefore, The probability that a randomly selected student’s math score is between 300 and 700 is 0.9544.