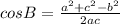Question

Law of cosines: a2 = b2 + c2 – 2bccos(A)

Which equation correctly applies the law of cosines to solve for an unknown angle measure?

Answer 1

`cos A = (b^2+c^2-a^2)/(2bc)`

Explanation:

Let us suppose a ΔABC , whose interior angles are A , B and C

Let their sides are measured as

a , b and c

where a is the side opposite to ∠A and so on.

Now there exist a formula , known as Law of cosine ,which helps us to determine the value of any angle , if all the sides of the triangle is given .

This formula is described as under

`cos A = (b^2+c^2-a^2)/(2bc)`

Above formula gives to cosine of ∠A, similarly we have formula for ∠B and ∠C

`cos B= (a^2+c^2-b^2)/(2ac)`

`cos C= (a^2+b^2-c^2)/(2ab)`