Answer:
1) Translated to left by 2 unit.
2) Translated down by 1 unit.
3) Compressed vertically by 1/2 unit.
Explanation:
Given : Graph of the function
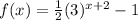
To find : How does f(x) relates to its parent function.
Solution : First we figure out its parent function
Parent function is the simplest form of the function.
f(x) parent function is
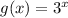
Now, how f(x) relates to g(x)
1. The parent function has been translated to the left.
Translated to left means
f(x)→f(x+b) , graph of f(x) has been translated by b unit.
In g(x)→g(x+2), graph of g(x) has been translated by 2 unit.
→The graph of g(x) has been translated to the left by 2 unit in the graph of f(x).
2)The parent function has been translated to the down.
Translated to down means
f(x)→f(x)-b , graph of f(x) has been translated left by b unit.
In g(x)→g(x)-1, graph of g(x) has been translated down by 1 unit.
→The graph of g(x) has been translated to the down by 1 unit in the graph of f(x).
3)The parent function has been compressed.
Compressed means
f(x)→a g(x) , graph of f(x) has been compressed by a unit.
In g(x)→(1/2)f(x), graph of g(x) has been compressed vertically by 1/2 unit.
→The graph of g(x) has been compressed vertically by 1/2 unit in the graph of f(x).