Question

a golfer tees off and hits a golf ball at a speed of 31 m/s and an angle of 35 degrees. how far did the ball travel before hitting the ground (answer) meters

Answer 1

Ans: R = Ball Travelled = 92.15 meters.

Step-by-step explanation:
First we need to derive that formula for the "range" in order to know how far the ball traveled before hitting the ground.

Along x-axis, equation would be:

`x = x_o + v_o_xt + (at^2)/(2)`

Since there is no acceleration along x-direction; therefore,

`x = x_o + v_o_xt`

Since
`v_o_x = v_ocos \alpha` and
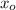
`x_o`=0; therefore above equation becomes,


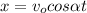
`x = v_ocos \alpha t` --- (A)

Now we need to find "t", and the time is not given. In order to do so, we shall use the y-direction motion equation. Before hitting the ground y ≈ 0 and a = -g; therefore,

=>
`y = y_o + v_o_yt - (gt^2)/(2)`
=>
`t = (2v_o_y)/(g)`

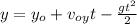
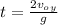
Since
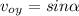
`v_o_y = sin \alpha`; therefore above equation becomes,

`t = (2v_osin \alpha )/(g)`

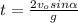
Put the value of t in equation (A):

(A) =>
`x = v_ocos \alpha (2v_osin \alpha )/(g)`

Where x = Range = R, and
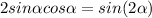
`2sin \alpha cos \alpha = sin(2 \alpha )`; therefore above equation becomes:

=>
`R = (v_o)^2 *(sin(2 \alpha ))/(g)`

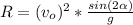
Now, as:

`v_o = 31 m/s`

and
`\alpha = 35`°
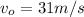
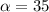
and g = 9.8 m/(s^2)

Hence,

`R = (31)^2 *(sin(2 *35 ))/(9.8)`

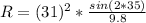Ans: R = 92.15 meters.

-i