Ans: R = Ball Travelled = 92.15 meters.
Step-by-step explanation:
First we need to derive that formula for the "range" in order to know how far the ball traveled before hitting the ground.
Along x-axis, equation would be:
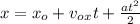
Since there is no acceleration along x-direction; therefore,
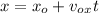
Since
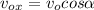
and
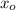
=0; therefore above equation becomes,
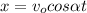
--- (A)
Now we need to find "t", and the time is not given. In order to do so, we shall use the y-direction motion equation. Before hitting the ground y ≈ 0 and a = -g; therefore,
=>
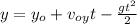
=>
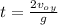
Since
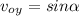
; therefore above equation becomes,
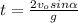
Put the value of t in equation (A):
(A) =>
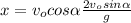
Where x = Range = R, and
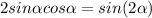
; therefore above equation becomes:
=>
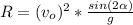
Now, as:
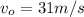
and
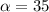
°
and g = 9.8 m/(s^2)
Hence,
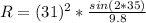 Ans: R = 92.15 meters.
Ans: R = 92.15 meters.-i