Question

Let f(x)=−1/2(x+2)^2+5 . What is the average rate of change for the quadratic function from x=−3 to x = 1? Enter your answer in the box. Show your work

Answer 1

Average rate of change= [ f(1)-f(-3) ] / [1-(-3) ]
Average rate of change= [ f(1)-f(-3) ] / (1+3)
Average rate of change= [ f(1)-f(-3) ] / (4)

x=1→f(1)=-1/2(1+2)^2+5
f(1)=-1/2(3)^2+5
f(1)=-1/2(9)+5
f(1)=-(1*9)/2+5
f(1)=-9/2+5
f(1)=(-9+2*5)/2
f(1)=(-9+10)/2
f(1)=1/2

x=-3→f(-3)=-1/2(-3+2)^2+5
f(-3)=-1/2(-1)^2+5
f(-3)=-1/2(1)+5
f(-3)=-(1*1)/2+5
f(-3)=-1/2+5
f(-3)=(-1+2*5)/2
f(-3)=(-1+10)/2
f(-3)=9/2

Average rate of change= [ f(1)-f(-3) ] / (4)
Average rate of change= [ 1/2-9/2 ] / (4)
Average rate of change= [ (1-9) /2 ] / (4)
Average rate of change= [ (-8) /2 ] / (4)
Average rate of change= (-4) / (4)
Average rate of change= -1

Answer: The average rate of change for the quadratic function from x=−3 to x = 1 is equal to -1

Answer 2

Ans: Average rate of change of function = -1

Step-by-step explanation:
The average rate of change of function f over the interval
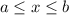
`a \leq x \leq b` is given as:

=> Average rate of change of function =
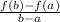
`(f(b) - f(a))/(b-a)` --- (A)

Since,
a = -3
b = 1

Given function =
`f(x) = - ((x+2)^2)/(2) +5`

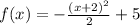
Therefore,

`f(b) = - ((b+2)^2)/(2) +5`
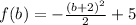
Since b = 1; therefore,

`f(b) = f(1) = - ((3)^2)/(2) +5 = (1)/(2)`



`f(a) = - ((a+2)^2)/(2) +5`
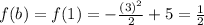
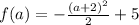
Since a = -3; therefore,

`f(a) = f(-3) = - ((-1)^2)/(2) +5 = (9)/(2)`

Plug-in the values of f(a), f(b), a, and b in equation (A):

(A) => Average rate of change of function =
`( (1)/(2) - (9)/(2) )/(1-(-3))`

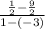
=> Ans: Average rate of change of function = -1

-i