Question

The function f(x) = 200 × (1.098)x represents a village's population while it is growing at the rate of 9.8% per year. Create a table to show the village's population at 0, 2, 4, 6, 8, and 10 years from now. Use your table to create a graph that represents the village's population growth. When the population doubles from its current size, the village will need to dig a new water well. To the nearest half of a year, about how long before it is time for the village to dig the new well?

Answer 1

a) See the attached for a table and graph.

b) It will be 7.5 years before it is time to dig a new well.

Answer 2

`f(x)= 200 * (1.098)^x`

`f(x)=200 *(1+(9.8)/(100))^x`

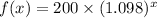
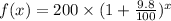
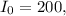`I_(0)=200,`, R= 9.8%,

Time =x=0,2,4,6,8,10

At, x=0

`I_(0)=200 * (1.098)^0=200`

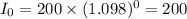
At, x=2

`I_(2)=200 * (1.098)^2=241.1208`

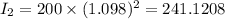
At, x=4

`I_(4)=200 * (1.098)^4=290.696`

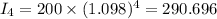
At, x=6

`I_(6)=200 * (1.098)^6=350.464`

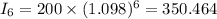
At, x=8

`I_(8)=200 * (1.098)^8=422.521`

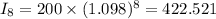
At, x=10

`I_(10)=200 * (1.098)^(10)=509.393`

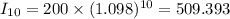
We will draw the graph of ,
`f(x)= 200 * (1.098)^x`.

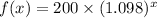So, New Population, when population of village doubles=400

`I_(P)=400\\\\ 400=200* (1.098)^x\\\\ 2=(1.098)^x\\\\ x=(log2)/(log1.098)`

`x=(0.30102)/(0.04060)\\\\ x=7.414`

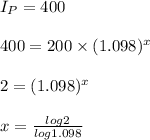
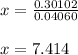
So, it take approximately, 7 years and approximately 146 days that is 7.414 years by the village to dig the new well.