Solution:
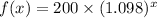
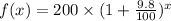
 , R= 9.8%,
, R= 9.8%,
Time =x=0,2,4,6,8,10
At, x=0

At, x=2
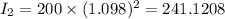
At, x=4
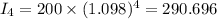
At, x=6

At, x=8
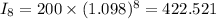
At, x=10
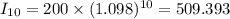
We will draw the graph of ,
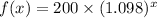 .
.
So, New Population, when population of village doubles=400
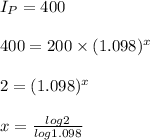
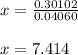
So, it take approximately, 7 years and approximately 146 days that is 7.414 years by the village to dig the new well.