Question

PR and PS are tangent to center Q. Find the measurement of angle Q.

Answer 1

Given, in the figure PR and PS are two tangents. They meet at P. Here angle P given. ∠P = 42°.

If we take a straight line PQ, it will create two triangles.

We can see here angle R and angle S both are right angles.

As here two triangles, so sum of all the angles of the triangles is
`180^o + 180^o = 360^o`

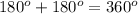
Now if we subtract the two right angles we will get,

`360^o-90^o-90^o = 360^o-180^o = 180^o`

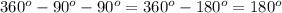
That means ∠P+∠Q = 180°

If we substitute the value of angle P we will get,

`42^o+Q = 180^o`

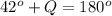
We can get angle Q by subtracting 42 to both sides. We will get,

`42^o+Q-42^o = 180^o-42^o`

`Q = 180^o-42^o`

`Q = 138^o`

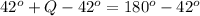
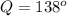
So we have got angle Q, the measurement of ∠Q = 138°.

Answer 2

Angle Q is supplementary to angle P (42°), so is 138°.