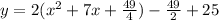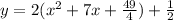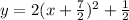Question

Which equation is y = (x + 3)2 + (x + 4)2 rewritten in vertex form?

Answer 1

Answer: B on edge 2020.

Explanation:

Answer 2

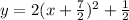`y=2(x+(7)/(2))^2+(1)/(2)` vertex form

Explanation:

`y = (x + 3)^2 + (x + 4)^2`

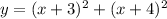
Lets square the terms

`(x+3)^2=x^2+6x+9`

`(x+4)^2= x^2+8x+16`

`y = x^2+6x+9 +x^2+8x+16=2x^2+14x+25`

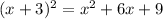
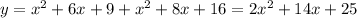
Now use completing the square method to get the vertex form

to apply the method we need to take out 2

WE take middle term , divide it by 2 and square it . then add and subtract it

`y =2(x^2+7x)+25`

`(7)/(2)`

square it
`(49)/(4)`

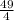
Add and subtract the fraction

`y=2(x^2+7x+(49)/(4)-(49)/(4))+25`

Take out -49/4 and multiply with 2 , then add it with 25

`y=2(x^2+7x+(49)/(4))-(49)/(2)+25`

`y=2(x^2+7x+(49)/(4))+(1)/(2)`

`y=2(x+(7)/(2))^2+(1)/(2)`