Here the expression given,
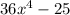 . We have to factorise the expression.
. We have to factorise the expression.
We know that 36 is a perfect square as
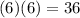 , that means
, that means
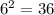 .
.
Similarly,
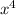 is also a perfect square, as
is also a perfect square, as
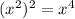 .
.
25 is also a perfect square, as

So we can write,

=
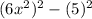
We will use the formula of diffference of two squares now. The formula is,
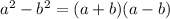
By using this formula we will get
 , so we can write,
, so we can write,
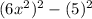 =
=
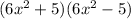
We have got the required answer. First option is correct here.