Answer:
(D) LP⊥PN
Explanation:
A rectangle is a parallelogram with four right angles., thus in order to prove that LMNP is rectangle, we have to show that LP is perpendicular to PN.
The coordinates of vertices are L(-4,1), P(-3,-1) and N(3,2), then

⇒
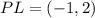
And,
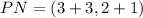
⇒
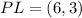
Now, taking the dot product, we have
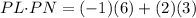
⇒
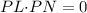
Since the dot product of two vectors is equal to zero, these vectors are perpendicular.
Also, It is given that LMNP is a parallelogram , therefore
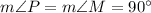 and
and
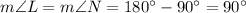
Thus, all the angles of the given parallelogram are equal and are equal to 90°, therefore LMNP is a rectangle.
Hence proved.
Thus, option D is correct.