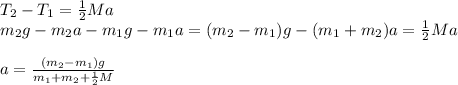Question

In the figure below the pulley is a solid disk of mass M and radius R with rotational inertia MR 2/2. Two blocks one of mass m and one of mass 2 hang from either side of the pulley by a light cord. Initially the system is a test with block one on the floor and block two held at the height h above the floor. Block 2 is then released and allowed to fall. Give your answers in terms of m, m2' M, R, h, and g

Answer 1

Assuming you are looking for the acceleration a:

1.
`m_1a = T_1 -m_1g`
2.
`m_2a = m_2g - T_2`
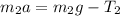
where T is the tension and a is the acceleration of the blocks. The acceleration of the two blocks and the acceleration of the pulley must be equal.

The torque on the pulley is given by:
3.
`\tau = \overrightarrow r * \overrightarrow F = (T_2 - T_1)R = I\alpha = (1)/(2) MR^2 (a)/(R)`
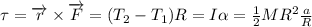
where
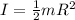
`I = (1)/(2) mR^2` and
`a = \alpha R`.

Combining the three equations:

`T_2 - T_1 = (1)/(2) Ma \\ m_2g - m_2a -m_1g - m_1a = (m_2-m_1)g - (m_1 + m_2)a = \frac{1}2}Ma \\ \\ a = ((m_2 - m_1)g)/(m_1 + m_2 + (1)/(2)M )`