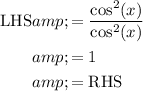a.)
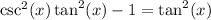
Use the identities
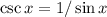
and
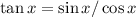
on the left-hand side
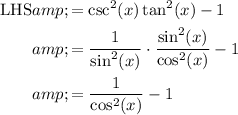
Make 1 have a common denominator to allow for fraction subtraction
Multiply the numerator and denominator of 1 by cos^2 x
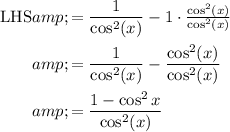
Use Pythagorean identity for the numerator.
If
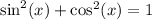
then subtracting both sides by
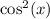
yields
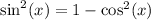
. We can substitute that into the numerator
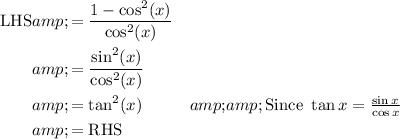
======
b.)
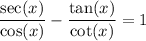
For the left-hand side:
By definition,
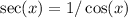
and
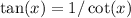
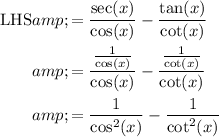
Since
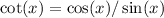
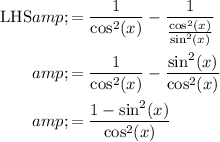
Using Pythagorean identity,
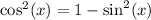
so