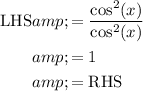Question

Prove that:

a.) [csc^2(x)] * [tan^2(x)] -1 = [tan^2 (x)]

b.) Sec(x)/Cos(x) - tan(x)/cot(x) = 1

Show all your work for both the equations!

Answer 1

a.)


`\csc^2(x) \tan^2 (x)- 1 = \tan^2(x)`

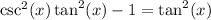
Use the identities
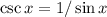
`\csc x = 1 / \sin x` and
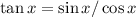
`\tan x = \sin x / \cos x` on the left-hand side


`\begin{aligned} \text{LHS} &= \csc^2(x) \tan^2 (x)- 1 \\ &= (1)/(\sin^2 (x)) \cdot (\sin^2 (x))/(\cos^2 (x)) - 1 \\ &= (1)/(\cos^2 (x)) - 1 \end{aligned}`

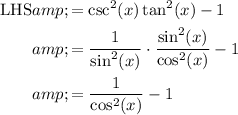
Make 1 have a common denominator to allow for fraction subtraction
Multiply the numerator and denominator of 1 by cos^2 x


`\begin{aligned} \text{LHS} &= (1)/(\cos^2 (x)) - 1 \cdot \tfrac{\cos^2 (x)}{\cos^2 (x)} \\ &= (1)/(\cos^2 (x)) - (\cos^2 (x))/(\cos^2 (x)) \\ &= (1 - \cos^2 x)/(\cos^2 (x)) \end{aligned}`

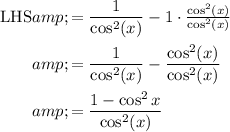
Use Pythagorean identity for the numerator.

If
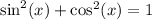
`\sin^2 (x) + \cos^2(x) = 1` then subtracting both sides by
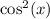
`\cos^2 (x)` yields
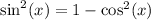
`\sin^2(x) = 1 - \cos^2(x)`. We can substitute that into the numerator


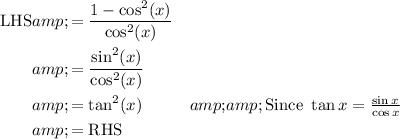
`\begin{aligned} \text{LHS} &= (1 - \cos^2 (x))/(\cos^2 (x)) \\ &= (\sin^2 (x))/(\cos^2 (x)) \\ &= \tan^2 (x) && \text{Since } \tan x = \tfrac{\sin x }{\cos x} \\ &= \text{RHS} \end{aligned}`

======

b.)


`(\sec(x))/(\cos(x)) - (\tan(x))/(\cot(x)) = 1`

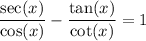
For the left-hand side:
By definition,
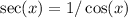
`\sec(x) = 1/\cos(x)` and
`\tan (x) = 1/\cot (x)`


`\begin{aligned} \text{LHS} &= (\sec(x))/(\cos(x)) - (\tan(x))/(\cot(x)) \\ &= ( (1)/(\cos(x)) )/(\cos(x)) - ((1)/(\cot(x)))/(\cot(x)) \\ &= (1)/(\cos^2 (x)) - (1)/(\cot^2(x)) \end{aligned}`

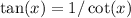
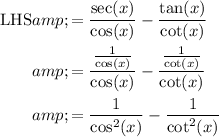
Since
`\cot (x) = \cos (x) / \sin (x)`


`\begin{aligned} \text{LHS} &= (1)/(\cos^2 (x)) - (1)/((\cos^2(x))/(\sin^2(x)) ) \\ &= (1)/(\cos^2 (x)) -(\sin^2(x))/(\cos^2(x)) \\ &= (1 - \sin^2(x))/(\cos^2 (x)) \end{aligned}`

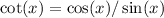
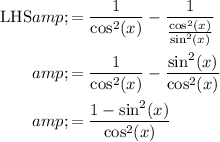
Using Pythagorean identity,
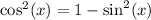
`\cos^2(x) = 1 - \sin^2(x)` so


`\begin{aligned} \text{LHS} &= (\cos^2(x))/(\cos^2 (x)) \\ &= 1 \\ &= \text{RHS} \end{aligned}`