Answer:
Minimum: y=-106. Maximum: infinite
Explanation:
The function described is a parabola, written in the form:
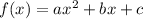
with:
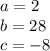
First of all, we notice that the parabola is upward, because the sign of the coefficient of the second-order term (a) is positive (in fact, a=2). Therefore, it has a minimum value of y. The x corresponding to the vertex of the parabola is given by:
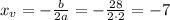
And substituting into f(x), we find the minimum value of y:
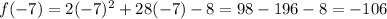
While the parabola has no maximum value, since it goes to infinite as x becomes larger.