Question

The front of a storage bunker can be modeled by y=-5/216(x-72)(x+72), where x and y are measured in inches. The x axis represents the ground. Find the width of the bunker at ground level.

Answer 1

The width of the bunker at ground level is 14.58 inches.

Step-by-step explanation:

The x-axis is the ground level, so the y-axis must be the scale for the length. Using the provided model, the x-intercepts, namely where the x-axis gets touched, we can just get the distance between them and that's the ground-level width.

The width of the bunker at ground level can be found by substituting x = 0 into the equation y = -5/216(x-72)(x+72).

This equation represents a quadratic function, which means it is a parabola.

By substituting x = 0, we get y = -5/216(-72)(72)

= 14.58 inches.

Answer 2

as far as I can make out this one.

the bunker is a 3D object, it has a height, with and length, however we're only concerned with the 2D front face, which has a length and width only.

we know the x-axis is the ground level, so the y-axis must be the scale for the length.

if we can find, using the provided model, the x-intercepts, namely where the x-axis gets touched, we can just get the distance between them and that's the ground level width.

keeping in mind that when the graph touches the x-axis, an x-intercept, "y" is 0.


`\bf y=-\cfrac{5}{216}(x-72)(x+72)\implies \stackrel{y}{0}=-\cfrac{5}{216}(x-72)(x+72) \\\\\\ 0=\stackrel{\textit{difference of squares}}{(x-72)(x+72)}\implies 0=x^2-72^2\implies 72^2=x^2 \\\\\\ \pm√(72^2)=x\implies \pm 72=x`

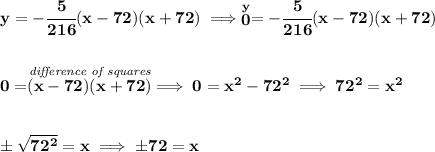
now, the distance from (-72, 0) and (72, 0) is just 72 +72, or 144.