as far as I can make out this one.
the bunker is a 3D object, it has a height, with and length, however we're only concerned with the 2D front face, which has a length and width only.
we know the x-axis is the ground level, so the y-axis must be the scale for the length.
if we can find, using the provided model, the x-intercepts, namely where the x-axis gets touched, we can just get the distance between them and that's the ground level width.
keeping in mind that when the graph touches the x-axis, an x-intercept, "y" is 0.
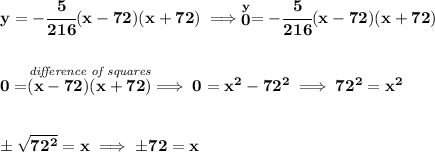
now, the distance from (-72, 0) and (72, 0) is just 72 +72, or 144.