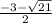Lets get started :)
These questions have asked us to solve by completing the square.
How do we? I have attached a picture, which will explain
6. x² + 2x = 8
→ b is the coefficient of x, which is 2
→ We take half of 2 and square it. Then, we add it to either side
x² + 2x
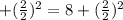
x² + 2x + 1 = 8 + 1
( x + 1 )( x + 1 ) = 9
( x + 1 )² = 9
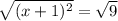 x + 1 = + 3 or x + 1 = - 3 x = 2 or x = - 4
x + 1 = + 3 or x + 1 = - 3 x = 2 or x = - 47. x² - 6x = 16
→ We do the same thing we did in the previous question
x² - 6x +

x² - 6x + 9 = 16 + 9
(x - 3)² = 25
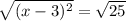 x - 3 = + 5 or x - 3 = - 5 x = 8 or x = - 2
x - 3 = + 5 or x - 3 = - 5 x = 8 or x = - 28. x² - 18x = 19
x² - 18x +
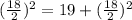
x² - 18x + 81 = 19 + 81
( x - 9 )( x - 9 ) = 100
( x - 9 )² = 100
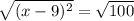
x - 9 = + 10 or x - 9 = -10
x = 19 or x = - 1
9. x² + 3x = 3
x² + 3x +
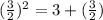

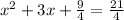
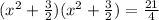
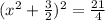
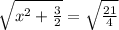 x +
x +
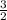 = +
= +
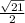 or x +
or x +
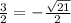 x =
x =
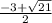 or x =
or x =