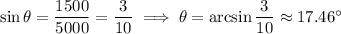In 22, you're looking for the vertical height of the triangle. You're given the angle opposite the side you want to find (which I'll call

) and the length of the hypotenuse. This sets you up with the relation
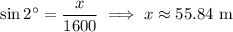
In 23, you're given a similar situation, except now you're looking for the angle (I'll call it
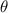
) in the triangle opposite the side denoting the height of the airplane. So this time,