Question

Suppose x follows a distribution with density function: \begin{equation} f\left(x\right) = \left\{\begin{array}{rl} c\left|x - 2\right|,& 0 \le x \le 3\\ 0, & \text{otherwise}\\ \end{array}\right. \end{equation} (note: for this question you can enter your answer in decimals as well as fractions.) what must the value of c be so that f(x) is a probability density function? tries 0/5 find the cumulative distribution function of f(x) for $ 2 \leq x \leq 3 $. [ the accepted form of answer is an algebraic expression in terms of "x". all algebraically equivalent expressions to the correct answer are accepted. write product as *

e.g 2*3 or 3*x, index/power as superscript,
e.g 2^3 for 2 raised to the power 3, the exponential function as exp(x), the logarithm function as log(x) (and not as ln(x)) ] tries 0/5 find the median of the probability distribution of x tries 0/2 find e(x) tries 0/5 find the cumulative distribution function of f(x) for $ 0 \leq x \leq 2 $. [ the accepted form of answer is an algebraic expression in terms of "x". all algebraically equivalent expressions to the correct answer are accepted. write product as *
e.g 2*3 or 3*x, index/power as superscript,
e.g 2^3 for 2 raised to the power 3, the exponential function as exp(x), the logarithm function as log(x) (and not as ln(x)) ]

Answer 1

The question is a bit of a mess, so here's an attempt at parsing out the relevant information.

Given the PDF of a random variable
`X`:


`f_X(x)=\begin{cases}c|x-2|&\text{for }0\le x\le3\\0&\text{otherwise}\end{cases}`

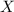
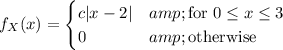
Find
`c`, the CDF, the median of
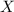
`X`, and the expectation of
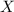
`X` (in no particular order).

For
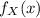
`f_X(x)` to be valid PDF, we require


`\displaystyle\int_(-\infty)^\infty f_X(x)\,\mathrm dx=1`

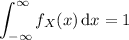
Note that


`|x-2|=\begin{cases}x-2&\text{for }x\ge2\\2-x&\text{for }x<2\end{cases}`

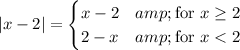
We have


`\displaystyle\int_(-\infty)^\infty f_X(x)\,\mathrm dx=c\int_0^3|x-2|\,\mathrm dx=c\int_0^2(x-2)\,\mathrm dx+c\int_2^3(2-x)\,\mathrm dx`

`\implies\frac{5c}2=1\implies c=\frac25`

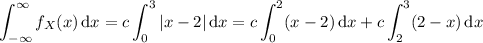
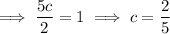
The CDF is defined by


`F_X(x)=\mathbb P(X\le x)=\displaystyle\int_(-\infty)^xf_X(t)\,\mathrm dt`

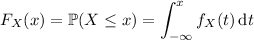
To find the CDF, we compute the integral above for the four possible cases:


`x<0\implies\displaystyle\int_(-\infty)^xf_X(t)\,\mathrm dt=0`

`0\le x<2\implies\displaystyle\int_(-\infty)^xf_X(t)\,\mathrm dt=c\int_0^x|t-2|\,\mathrm dt=\frac{4x-x^2}5`

`2\le x<3\implies\displaystyle\int_(-\infty)^xf_X(t)\,\mathrm dt=\frac45+c\int_2^x|t-2|\,\mathrm dt=\frac45-c\int_2^x(2-t)\,\mathrm dt=\frac{8-4x+x^2}5`

`x\ge3\implies\displaystyle\int_(-\infty)^xf_X(t)\,\mathrm dt=1`

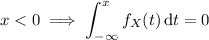
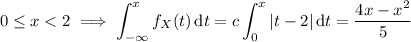
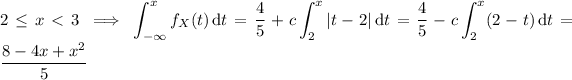
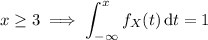
So the CDF is


`F_X(x)=\begin{cases}0&\text{for }x<0\\\\\frac{4x-x^2}5&\text{for }0\le x<2\\\\\frac{8-4x+x^2}5&\text{for }2\le x<3\\\\1&\text{for }x\ge3\end{cases}`

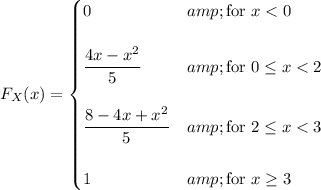
The median is the value
`M` such that
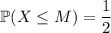
`\mathbb P(X\le M)=\frac12`. From the PDF, we can gather that the median must fall somewhere in
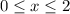
`0\le x\le2`. The CDF then tells us that


`\mathbb P(X\le M)=F_X(M)=\frac12=\frac{4M-M^2}5\implies M=2-√(\frac32)\approx0.775`

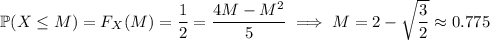
The expected value of
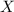
`X` is given by


`\mathbb E[X]=\displaystyle\int_(-\infty)^\infty x\,f_X(x)\,\mathrm dx`

We have


`\mathbb E[X]=\displaystyle\frac25\int_0^2x(x-2)\,\mathrm dx+\frac25\int_2^3x(2-x)\,\mathrm dx=(16)/(15)`