Question

One number is 4 less than twice a second number. find a pair of such numbers so that their product is as small as possible.

Answer 1

Numbers are -2 and 1.

Explanation:

Let x be the second number,

⇒ First number = 4 less than twice a second number

= 2 × Second number - 4

= 2x - 4

Thus, the product of first and second number is,

`f(x) = x(2x-4)`

`\implies f(x) = 2x^2 - 4x`

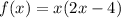
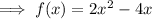
Differentiating with respect to x,

`f'(x) = 4x -4`

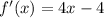
Again differentiating with respect to x,

`f''(x) = 4`

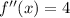
Now, for maximum or minimum,

`f'(x)=0`

`\implies 4x - 4 = 0\implies 4x = 4\implies x = 1`

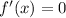
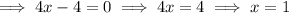
Since, for x = 1, f''(x) = Positive,

Therefore, the function f(x) is minimum for x = 1,

⇒ The product is smallest for x = 1,

Hence, the second number = x = 1,

And, first number = 2x - 4 = 2 - 4 = -2

Answer 2

For this case, the first thing we must do is define a variable.
We have then:
x: unknown number.
First number: 2x - 4
Second number: x
The product of the numbers is:

`y = x (2x-4)`
Rewriting:

`y = 2x ^ 2-4x`
Deriving the equation we have:

`y '= 4x-4`
We equal zero and clear x:

`4x - 4 = 0 x = 4/4 x = 1`
Then, the first number is:

`2x - 4 = 2 (1) - 4 = 2 - 4 = - 2`
Answer:
First number: -2
Second number: 1