Question

Find the side and measure B

Answer 1

When angle opposite to the unknown sides and other two sides are given then we use law of cosines

Law of cosine

`c^2 = a^2 + b^2 - 2ab cos(c)`

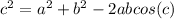
From the given diagram

`AB^2 = CB^2 + AC^2 - 2(CB)(AC) cos( c)`

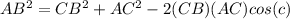
CB = 108

AC= 55

Angle c= 59

`AB^2 = 108^2 + 55^2 - 2(108)(55) cos( 59 )`

`AB^2 = 8570.34767`

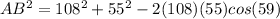
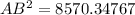
Take square root on both sides

AB = 92.6 m

To find out angle B we use sine law

`(sin(a))/(a) = (sin b)/(b) = (sin c)/(c)`

`(sin b)/(b) = (sin c)/(c)`

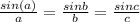
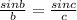
From the figure

`(sin B)/(AC) = (sin C)/(AB)`

`(sin B)/(55) = (sin 59)/(92.6)`

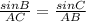
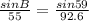
sin(B) = 0.50916647

B =
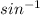`sin^(-1)`(0.50916647)

Angle B= 30.61 degrees