Question

Will fan and medal. How is this correct?

3. A family is building a circular fountain in the backyard. The yard is rectangular and measures 7x by 6x and the fountain is going to be circular with a radius of 2x. Once the fountain is build, what will be the area of the remaining yard?
A. 38x^2
B. [x] 2x^2 (21 – 2pi)
C. 42x^2 – 2pix^2
D. 38pix^2,

Answer 1

Step
`1`

Find the area of the rectangular yard

the area of the rectangular yard is equal to

`A=L*W`

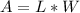
where

L is the length side of the rectangle

W is width side of the rectangle

in this problem we have

`L=7x\ units\\W=6x\ units`

`A=L*W`

`A=7x*6x`

`A=42x^(2)\ units^(2)`

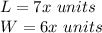
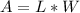
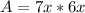
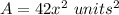
Step
`2`

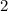
Find the area of a circular fountain

we know that

the area of a circle is equal to

`A=\pi r^(2)`

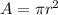
where

r is the radius of the circle

in this problem we have

`r=2x\ units`

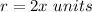
substitute

`A=\pi (2x)^(2)`

`A=4\pi x^(2)\ units^(2)`

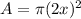
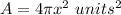
Step
`3`

Find area of the remaining yard

Subtract the area of a circular fountain from the area of the rectangular yard

`42x^(2)\ units^(2)-4 \pi x^(2)\ units^(2)=2x^(2)[21-2\pi]`

therefore

the answer is the option B

`2x^(2)[21-2\pi]\ units^(2)`

Answer 2

The yard is rectangular with a measurement of 7x by 6x.
The fountain is circular with a radius of 2x.
Since we are looking for the remaining area, we need to know the area of the rectangular backyard and the circular fountain.

The formula for a rectangle is
A=lw
where:
l=length
w=width

So,
A=(7x)(6x)
=42x^2

Now for the area of the circular fountain,
A=