Step

Find the area of the rectangular yard
the area of the rectangular yard is equal to
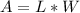
where
L is the length side of the rectangle
W is width side of the rectangle
in this problem we have
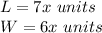
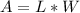
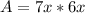
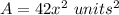
Step
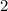
Find the area of a circular fountain
we know that
the area of a circle is equal to
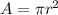
where
r is the radius of the circle
in this problem we have
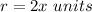
substitute
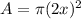
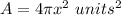
Step
Find area of the remaining yard
Subtract the area of a circular fountain from the area of the rectangular yard
![42x^(2)\ units^(2)-4 \pi x^(2)\ units^(2)=2x^(2)[21-2\pi]](https://img.qammunity.org/2019/formulas/mathematics/high-school/d931k5djdx80h0vuxm8odtwn0q6hs305mb.png)
therefore
the answer is the option B
![2x^(2)[21-2\pi]\ units^(2)](https://img.qammunity.org/2019/formulas/mathematics/high-school/h3f99amd6d0u40kzuxlhvkhsu9l8id1a32.png)