Question

a 12-ft-long ladder is leaning against a wall and makes an 80 degree angle with the ground.how high up the wall does the ladder reach, and how far is the base of the ladder from the base of the wall? round to the nearest inch.,

Answer 1

Height of ladder = sin80 x h = 11 feet 10 inches Base of ladder to wall = cos80 x h = 2 feet 1 inch

Answer 2

The ladder reaches 142 inches and the base of ladder is 25 inches far from the base of the wall.

Explanation:

Let us draw a diagram for the given situation.

In the attached figure,

AB = the height of wall where the ladder reaches

AC = ladder

BC = distance of base of ladder from the base of the wall

In triangle ABC,

`\sin C=(AB)/(AC)\\\\\sin80=(AB)/(12)\\\\AB=12\sin80\\\\AB=11.82`

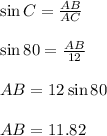
And

`\cos C=(BC)/(AC)\\\\\cos80=(BC)/(12)\\\\BC=12\cos80\\\\BC=2.08`

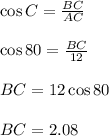
Now, 1 feet = 12 inches

Hence, 11.82 ft = 141.84 inches

and 2.08 feet = 24.96 inches

Therefore, in the nearest inches, we have

The ladder reaches 142 inches and the base of ladder is 25 inches far from the base of the wall.