Assume the first even integer is x.
The next even integer will be 2 digits after this digit. So the next even integer will be x+2.
The reciprocals of these two even integers can be written as
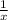
and
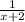
respectively.
The sum of their reciprocals is 7/24. So we can set up the equation as:
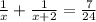
Taking LCM on left hand side:
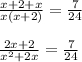
Cross Multiplying the denominators:
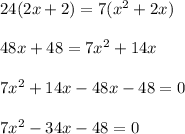
Using the quadratic formula to solve the above equation:
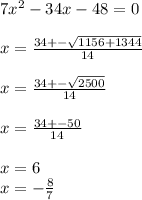
Since, the value of x can only be an integer, we discard the fractional value and keep x=6
So the first even integer is 6 and the next even integer is 8. The sum of reciprocals of 6 and 8 is 7/24