Question

The sum of the reciprocals of two consecutive even integers is 7/24. Write an equation that can be used to find the two integers. Find the two integers.

Answer 1

Assume the first even integer is x.
The next even integer will be 2 digits after this digit. So the next even integer will be x+2.

The reciprocals of these two even integers can be written as
`(1)/(x)` and
`(1)/(x+2)` respectively.

The sum of their reciprocals is 7/24. So we can set up the equation as:


`(1)/(x)+ (1)/(x+2)= (7)/(24)`

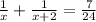
Taking LCM on left hand side:


`(x+2+x)/(x(x+2))= (7)/(24) \\ \\ (2x+2)/( x^(2) +2x)= (7)/(24)`

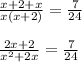
Cross Multiplying the denominators:


`24(2x+2)=7({ x^(2) +2x}) \\ \\ 48x+48=7 x^(2) +14x \\ \\ 7 x^(2) +14x-48x-48=0 \\ \\ 7 x^(2) -34x-48=0 \\ \\`

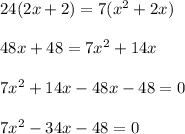
Using the quadratic formula to solve the above equation:

`7 x^(2) -34x-48=0 \\ \\ x= (34+- √(1156+1344) )/(14) \\ \\ x= (34+- √(2500) )/(14) \\ \\ x=(34+-50 )/(14) \\ \\ x=6 \\ x=- (8)/(7)`

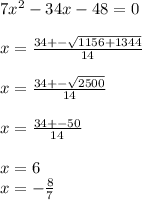
Since, the value of x can only be an integer, we discard the fractional value and keep x=6

So the first even integer is 6 and the next even integer is 8. The sum of reciprocals of 6 and 8 is 7/24