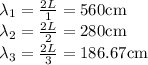Question

What are the three longest wavelengths for standing waves on a 280-cm-long string that is fixed at both ends? enter your answers numerically separated by commas?

Answer 1

Three longest wavelengths will correspond to the three modes of vibration that has the least amount of nodes. For a standing wave on a string fixed on both ends we have the following formula:

`\lambda_n=(2L)/(n); n=1,2,3,4,5,...`
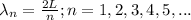
Where L is the length of a string and n is the number of nodes of the standing wave.
From this formula, we see that the more nodes you have the lower your wavelength is.
We need to calculate wavelengths for n=1, n=2, and n=3.

`\lambda_1=(2L)/(1)=560$cm\\ \lambda_2=(2L)/(2)=280$cm\\ \lambda_3=(2L)/(3)=186.67$cm\\`