Answer : C
the roots of the polynomial equation x^3-10x=-3x^2+24
We use a graphing calculator
Graph the left hand side expression using graphing calculator
We graph
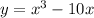
Then we graph the right hand side expression using graphing calculator
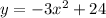
so we got two system of equations
The intersection of two graphs is our solution
The graph is attached below
We can see that the graph intersects at 3 points
(-4, -24) (-2,12) and (3,-3)
So the roots are -4, -2 , 3