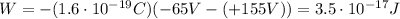Question

How much work does the electric field do in moving a proton from a point with a potential of +155 v to a point where it is -65 v ? express your answer in joules?

Answer 1

The work done by the electric field is equal to the loss of electric potential energy of the proton in moving from its initial location to its final location:

`W=-\Delta U = -q \Delta V = -q (V_f -V_i)`
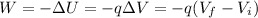
where
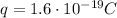
`q=1.6 \cdot 10^(-19)C` is the proton charge,
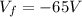
`V_f = -65 V` and
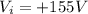
`V_i=+155 V` are the voltages in the final and initial locations. Substituting, we get

`W=-(1.6 \cdot 10^(-19)C)(-65 V-(+155 V))=3.5 \cdot 10^(-17)J`