First of all, let's convert the time interval into minutes. Since
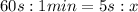
we find
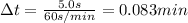
Then we can find the angular acceleration of the flywheel:
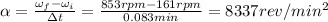
At this point, we can use the law of motion of an uniformly accelerated rotational motion. The angular displacement after a time
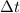
is given by
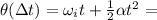
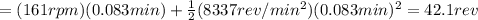
So, the flywheel covers 42.1 revolutions.