Question

A torque applied to a flywheel causes it to accelerate uniformly from a speed of 161 rev/min to a speed of 853 rev/min in 5.0 seconds. determine the number of revolutions n through which the wheel turns during this interval. (suggestion: use revolutions and minutes for units in your calculations.)

Answer 1

First of all, let's convert the time interval into minutes. Since

`60 s: 1 min = 5 s: x`
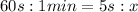
we find

`\Delta t = (5.0 s)/(60 s/min)=0.083 min`

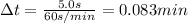
Then we can find the angular acceleration of the flywheel:

`\alpha = (\omega _f - \omega_i)/(\Delta t)= (853 rpm-161 rpm)/(0.083 min)=8337 rev/min^2`

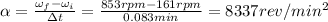
At this point, we can use the law of motion of an uniformly accelerated rotational motion. The angular displacement after a time
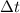
`\Delta t` is given by

`\theta (\Delta t)= \omega_i t + (1)/(2) \alpha t^2 =`

`=(161 rpm)(0.083 min)+ (1)/(2)(8337 rev/min^2)(0.083 min)^2 =42.1 rev`
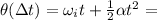
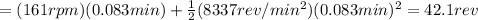
So, the flywheel covers 42.1 revolutions.