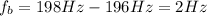Question

A guitar string has a linear density of 8.30 ✕ 10−4 kg/m and a length of 0.660 m. the tension in the string is 56.7 n. when the fundamental frequency of the string is sounded with a 196.0-hz tuning fork, what beat frequency is heard?

Answer 1

First of all, we need to find the fundamental frequency of the string.

The fundamental frequency of a string is given by:

`f_1 = (1)/(2L) \sqrt{ (T)/(\mu) }`
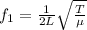
where L is the length of the string, T the tension and
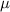
`\mu` the linear density.
Using the information given in the exercise: L=0.660 m, T=56.7 N and
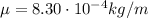
`\mu =8.30 \cdot 10^(-4) kg/m`, we find

`f_1 = (1)/(2\cdot 0.660 m) \sqrt{ (56.7 N)/(8.30 \cdot 10^(-4)kg/m) }=198 Hz`

The beat frequency is given by the difference in frequency between the fundamental frequency of the string and the tuning fork (196 Hz), so it is:

`f_b = 198 Hz - 196 Hz = 2 Hz`

Answer 2

Ans: Beat Frequency = 1.97Hz

Step-by-step explanation:
The fundamental frequency on a vibrating string is


`f = \sqrt{ (T)/(4mL) }` -- (A)

here, T=Tension in the string=56.7N,
L=Length of the string=0.66m,
m= mass = 8.3x10^-4kg/m * 0.66m = 5.48x10^-4kg


Plug in the values in Equation (A)

so
`f = \sqrt{ (56.7)/(4*5.48*10^(-4)*0.66) }` = 197.97Hz

the beat frequency is the difference between these two frequencies, therefore:
Beat frequency = 197.97 - 196.0 = 1.97Hz
-i