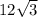Question

PLEASE explain this, I'm so lost. 25 points! What is the area of the base of the pyramid? Enter your answer in the box. Express your answer in radical form.

Answer 1

The answer is:

area of base =
`12√(3)`

Hope it helps!

Answer 2

To find the area of the triangle shown we have to find the length of a and the base.

a can be found using the sine function. Recall sin = (opp)/(hyp)

Here
`sin 60 = (a)/(8)`

`( √(3) )/(2)= (a)/(8)`

`2a=8 √(3)`

`a=4 √(3)`

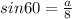
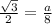
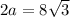
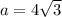
The base can be found using the sin of 30 degrees as this is a 30-60-90 right triangle.

`sin30= (b)/(8)`

`\ (1)/(2) = (b)/(8)`

`b=4`

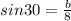
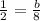
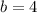
The area of the triangle in the picture is given by
`A=( (1)/(2) )bh= ((1)/(2))(4)( ( √(3) )/(2) )= √(3)`.

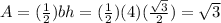
The base of the pyramid is a hexagon which can be divided into 6 triangles each of which is double the area of the one we just found. So the area of the base = 2(area of the triangle we found)(6) =
`12 √(3)`