Question

For a sine wave depicting simple harmonic motion, the smaller the amplitude of the wave, the smaller the of the pendulum from the equilibrium position. The shorter the period, the the pendulum’s rod.

Answer 1

displacement   , shorter 

Answer 2

The smaller the amplitude of the wave, the smaller the displacement of the pendulum from the equilibrium position. The shorter the period, the shorter the pendulum’s rod.

To find the right answer, we could look the analysis of a simple pendulum movement. The relation that defines this movement is:

`T=2 \pi \sqrt{(l)/(g) }`

`T: \ period\\l: \ pendulum's \ rod \ length\\g: \ gravity`

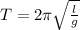
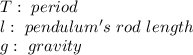
From the equation, we can see the relation between the period and the length of the pendulum's rod. They are directly proportional, this means that if the period increases, the length increases, or vice versa. So, the shorter the period, the shorter the pendulum's rod, because they are directly proportional.

On the other hand, the amplitude of the harmonic motion refers to the displacement of the object from the equilibrium point which is in the center of the periodic movement. This allow us to deduct that if the amplitude is small, the displacement of the object is small, if the amplitude is big, the displacement from the equilibrium point is bid.