Question

The function f(x) = 8(1/4)^x is reflected across the y-axis to create g(x). Which table of values could be used to graph g(x)?

Answer 1

It's the first one.

To reflect the function
`f(x)=8( (1)/(4))^(x)` about the y-axis, we write
`g(x)=8( (1)/(4))^(-x)`.

You can then substitute values into both functions. Remember that something to the power zero is equal one, so for either function evaluated at x = 0, the answer is 8.

Answer 2

Table 1

Explanation:

We have the function
`f(x)=8((1)/(4))^(x)`.

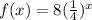Now, the function g(x) is obtained by reflecting f(x) across y-axis.

i.e. g(x) = f(-x)

i.e.
`g(x)=8((1)/(4))^(-x)`

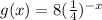
So, substituting the values of x in f(x) or g(x), we will discard some options.

2. For x=0, the value of
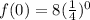`f(0)=8((1)/(4))^(0)` i.e. f(0) = 8.

As in table 2, f(0) = 0 is given, this is not correct.

3. For x=0, the value of
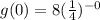`g(0)=8((1)/(4))^(-0)` i.e. g(0) = 8.

As in table 3, g(0) = -8 is given, this is not correct.

4. For x=0, the value of
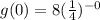`g(0)=8((1)/(4))^(-0)` i.e. g(0) = 8.

As in table 3, g(0) = 0 is given, this is not correct.

Thus, all the tables 2, 3 and 4 do not represent these functions.

Hence, table 1 represents f(x) and g(x) as the values are satisfied in this table.