Answer:
The area of remaining wall after the mural has been painted is
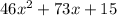 square units.
square units.
Explanation:
If the dimensions of a rectangle are l and w, then area of rectangle is
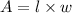
The dimensions of wall are (6x+7) and (8x+5). So, the area of wall is
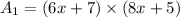



The dimensions of mural are (x+4) and (2x+5). So, the area of mural is
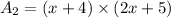
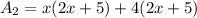
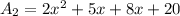
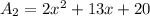
The area of remaining wall after the mural has been painted is
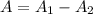
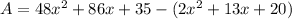
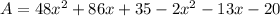
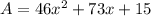
Therefore area of remaining wall after the mural has been painted is
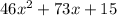 square units.
square units.