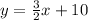Question

What is the slope-intercept form of the equation of the line that passes through the point (–6, 1) and is perpendicular to the graph of 2x + 3y = –5?

y = x – 8
y = x + 1
y = x + 1
y = x + 10

Answer 1

`y=(3)/(2)x+10`

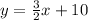
Explanation:

Given equation of line :
`2x + 3y = -5`

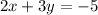
Standard form of equation of line =
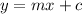`y=mx+c` ---A

Where m is the slope

Convert the given equation in standard form

`2x + 3y = -5`

`3y = -5-2x`

`y =(-5)/(3)-(2)/(3)x`

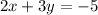
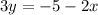
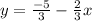
So, slope =
`m = -(2)/(3)`

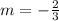
If the two lines are perpendicular then the product of their slopes is -1

Let n be the slope of required equation of line

So,
`m * n = -1`

`-(2)/(3)* n = -1`

`n=(3)/(2)`

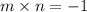
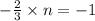
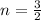
Substitute this value in A

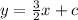`y=(3)/(2)x+c` --B

Now we are given that the required perpendicular line passes through the point (–6, 1)

So, substitute (–6, 1) in B

`1=(3)/(2)(-6)+c`

`1-((3)/(2)(-6))=c`

`10=c`

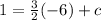
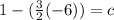
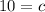
Substitute the value of c in B

`y=(3)/(2)x+10`

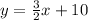
Hence the slope-intercept form of the equation of the line that passes through the point (–6, 1) and is perpendicular to the graph of 2x + 3y = –5? is
`y=(3)/(2)x+10`

Answer 2

When some line named l1 is perpendicular to some other line named l2 ,
then there is slope coefficijent

S1= - 1/ S2

In our case we must first transform given line from standard form to slope form

2x+3y= -5 => 3y = - 2x-5 => y = (-2/3)x -5

The slope coefficijent od the given line is S= - 2/3
Then the slope coefficijent of the requested line is

S1= - 1/(-2/3) => I suppose that you know to solve double fraction
S1=3/2
The equation for the line which passes through one point is
y-y1 = S1 (x-x1) => y-1 = 3/2 (x-(-6)) => y-1 =3/2 (x+6)
We will multiply both sides of the equation with number 2 and get
2y-2=3x+18 => 2y=3x+18+2 => 2y = 3x+20
When we divide the both sides with number 2 we finally get
y= (3/2)x+10.
Good luck!!!!