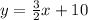Answer:
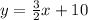
Explanation:
Given equation of line :
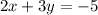
Standard form of equation of line =
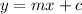 ---A
---A
Where m is the slope
Convert the given equation in standard form
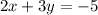
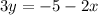
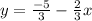
So, slope =
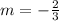
If the two lines are perpendicular then the product of their slopes is -1
Let n be the slope of required equation of line
So,
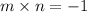
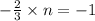
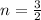
Substitute this value in A
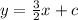 --B
--B
Now we are given that the required perpendicular line passes through the point (–6, 1)
So, substitute (–6, 1) in B
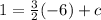
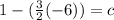
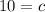
Substitute the value of c in B
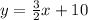
Hence the slope-intercept form of the equation of the line that passes through the point (–6, 1) and is perpendicular to the graph of 2x + 3y = –5? is