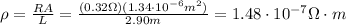Question

You apply a potential difference of 5.70 v between the ends of a wire that is 2.90 m in length and 0.654 mm in radius. the resulting current through the wire is 17.6

a. what is the resistivity of the wire?

Answer 1

1) First of all, let's find the resistance of the wire by using Ohm's law:

`V=IR`
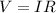
where V is the potential difference applied on the wire, I the current and R the resistance. For the resistor in the problem we have:

`R= (V)/(I)= (5.70 V)/(17.6 A)=0.32 \Omega`

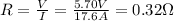
2) Now that we have the value of the resistance, we can find the resistivity of the wire
`\rho` by using the following relationship:

`\rho = (RA)/(L)`
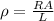
Where A is the cross-sectional area of the wire and L its length.
We already have its length
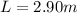
`L=2.90 m`, while we need to calculate the area A starting from the radius:

`A=\pi r^2 = \pi (0.654\cdot 10^(-3)m)^2=1.34 \cdot 10^(-6)m^2`

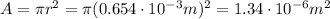
And now we can find the resistivity:

`\rho = (RA)/(L)= ((0.32 \Omega)(1.34 \cdot 10^(-6)m^2))/(2.90m)= 1.48 \cdot 10^(-7)\Omega \cdot m`