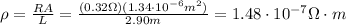1) First of all, let's find the resistance of the wire by using Ohm's law:
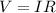
where V is the potential difference applied on the wire, I the current and R the resistance. For the resistor in the problem we have:
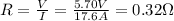
2) Now that we have the value of the resistance, we can find the resistivity of the wire
by using the following relationship:
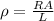
Where A is the cross-sectional area of the wire and L its length.
We already have its length
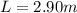
, while we need to calculate the area A starting from the radius:
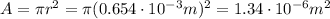
And now we can find the resistivity: