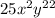Question

Choose the correct simplification of the expression (5xy5)2(y3)4. 25x2y22 10x2y22 25x3y14 10x3y14

Answer 1

Option A) 25x^2y^22

Explanation:

Answer 2

A)
`25x^2y^(22)`

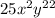
Explanation:

The given expression is
`(5xy^(5))^2 . (y^3)^4`

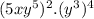
Here we have to use exponent rules and simplify the expression.

Power rule :
`(a^m)^n = a^(mn)`

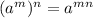
Using the above rule, we can write

`(5xy^(5) )^2 = 5^2.x^2.y^(5*2)`

=
`25.x^2.y^10`

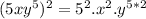
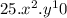
Again using the power rule

`(y^(3) )^4 = y^12`

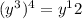
Now we have to put together this expression, we get

=
`25.x^2.y^(10) .y^(12)`

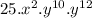
Now we have to use product rule.

Product rule:
`a^m . a^n = a^(m + n)`

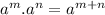
Using this rule, we can simplify further

=
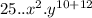
`25..x^2.y^(10 +12)`

=
`25x^2y^(22)`