Answer:
Hence, the length of the radius of a circle with center at origin is 17 units.
Explanation:
" We know that radius of a circle is any line segment joining center to any point on the circle ".
We have to find the length of the radius of a circle with a center at the origin i.e. (0,0) and a point on the circle at 8 + 15i i.e. at (8,15).
( Since any complex number of the form z=x+iy has a point in the coordinate plane as: (x,y) ).
Hence , we have to find the distance between the point (0,0) and (8,15).
The distance between two points (a,b) and (c,d) is given by:
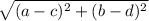
Here (a,b)=(0,0) and (c,d)=(8,15)
Hence distance between (0,0) and (8,15) is:
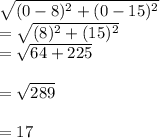
Hence, the length of the radius of a circle with center at origin is 17 units.