Question

Two large parallel conducting plates are 17 cm apart and have charges of equal magnitude and opposite sign on their facing surfaces. an electrostatic force of 2.9 ✕ 10-15 n acts on an electron placed anywhere between the two plate (neglect fringing). (a) find the electric field at the position of the electron.

Answer 1

The electrostatic force acting on a charge q is given by

`F=qE`
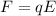
where E is the electric field's intensity.

In our problem, the particle is an electron, so its charge is
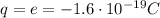
`q=e=-1.6 \cdot 10^(-19)C`. We know the intensity of the force, so we can find the magnitude of the electric field at the point where the electron is located:

`E= (F)/(q)= (2.9\cdot 10^(-15)N)/(-1.6 \cdot 10^(19)C)=-1.8 \cdot 10^4 N/C`
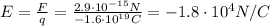
where the negative sign means that the force and the electric field have opposite direction, because the charge is negative.