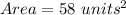Question

??????????????????????

Answer 1

`Area = 58 \ units^2`

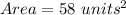
Explanation:

We can start by finding the third side of the triangle/the side of the square using the Pythagorean Theorem:

`a^2+b^2=c^2`

In this case the side length of the square would be represented by the variable "c" as it is the hypotenuse:

`3^2+7^2=c^2`

`9+49=c^2`

`c^2=58`

`c=√(58)`

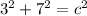
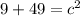
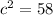
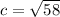
Since the area of a square is the side length square then...

`Area =( √(58) )^2`

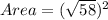
The square root and the squared cancel out giving us...

`Area = 58 \ units^2`