Question

The vertices of triangle ABC are A(2,3), B(–1,2), and C(3,1). If ΔDEF ∼ ΔABC and DE = 4AB, what is the length of EF? √10

Answer 1

If the length is 4 times from DE=4AB then the corresponding length of EF which is BC is also 4 times larger. Length of BC=sqrt((2-1)^2+(-1-3)^2)=sqrt of 17 Hence, length of EF is 1/4 of sqrt 17. Hope it helps

Answer 2

The length of EF is
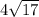`4√(17)` units.

Explanation:

The vertices of triangle ABC are A(2,3), B(–1,2), and C(3,1).

Using distance formula:

`D=√((x_2-x_1)^2+(y_2-y_1)^2)`

`BC=√((3+1)^2+(1-2)^2)=√(17)`

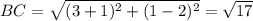
It is given that ΔDEF ∼ ΔABC.

If two triangles are similar then the corresponding sides are proportional.

`(AB)/(DE)=(BC)/(EF)`

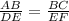
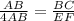`(AB)/(4AB)=(BC)/(EF)` (DE = 4AB)

`(1)/(4)=(BC)/(EF)`

`EF=4* BC`

`EF=4* √(17)`

`EF=4√(17)`

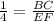
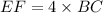
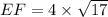
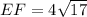
Therefore the length of EF is
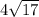`4√(17)` units.