Answer:
The length of EF is
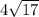 units.
units.
Explanation:
The vertices of triangle ABC are A(2,3), B(–1,2), and C(3,1).
Using distance formula:
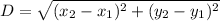
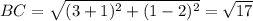
It is given that ΔDEF ∼ ΔABC.
If two triangles are similar then the corresponding sides are proportional.
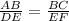
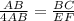 (DE = 4AB)
(DE = 4AB)
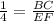
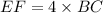
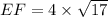
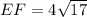
Therefore the length of EF is
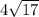 units.
units.