To find the solution set of a factored quadratic equation, you should set each one of the factors equal to zero and solve for

.
Lets take our first quadratic equation (x+1/2)(x-5)=0 and apply this. First we are our factors equal to zero
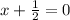
and
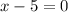
; next we are going to sole for

in each factor to find the solution set:

and
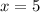
, so the solution set for the quadratic equation (x+1/2)(x-5)=0 is
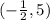
Lets do the same for our next one
(x-5)(2x-1)=0
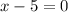
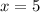
and
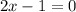
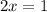

So, the solution set for the quadratic equation (x-5)(2x-1)=0 is
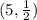
Next one (x+5)(2x-1)=0
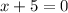

and
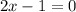
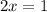

So, the solution set for the quadratic equation (x+5)(2x-1)=0 is
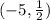
Next one (-2x+1)(-x+5)=0
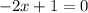
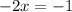
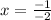

and
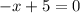
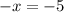
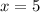
So, the solution set for the quadratic equation (-2x+1)(-x+5)=0 is
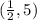 : therefore, we are going the select this one.
: therefore, we are going the select this one.
Next one (x+1/2)(x+5)=0
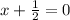

and
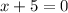

So, the solution set for the quadratic equation (x+1/2)(x+5)=0 is
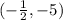
Finally, our last one (-2x+1)(x-5)=0
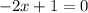
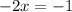
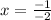

and
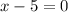
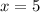
So, the solution set for the quadratic equation (-2x+1)(x-5)=0 is
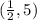 ; this is also a correct answer, make sure to select this one too.
; this is also a correct answer, make sure to select this one too.
We can conclude that both (-2x+1)(-x+5)=0 and (-2x+1)(x-5)=0 quadratic equation have
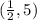 as solution set.
as solution set.